跳到主要内容

树

Tree

定义​

树是由n(n⩾0)n(n\geqslant0)个有限节点组成的具有层次关系的集合。
把它叫做“树”是因为它看起来像一棵倒挂的树
也就是说它是根在上，而叶在下的。

树的示例

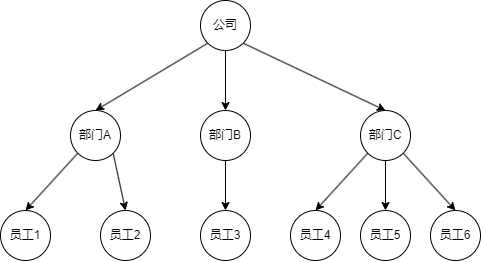
通用名词​

  • 节点（结点）：树的最小单元
  • 子树（子节点）：一个节点下面直接相连的节点
  • 节点的度：子树数量
  • 树的度：度最大的那个节点的度
  • 叶子（终端节点）：没有子树的节点
  • 非终端节点（分支节点）：有子树的节点。除根节点以外的非终端节点称为内部节点
  • 双亲，孩子，兄弟，祖先，子孙，堂兄弟：同层的都叫堂兄弟，其他不解释
  • 层次：根为第一层，孩子层次=双亲层次+1
  • 深度：树的最大层次
  • 有序树和无序树：若将树中每个结点的各子树看成是从左到右有次序的，则为有序树，否则为无序树
  • 空树：一个节点都没有的树

存储结构​

双亲表示法（顺序表）
孩子表示法（顺序表+链表）

孩子兄弟表示法（二叉树表示法）（二叉链表）
如下：
原树为A，转换后的二叉树为B
在B中
B中节点的左子树代表A中源节点的子树
B中节点的右子树代表A中源节点的兄弟

//---树的二叉链表存储表示---//
typedef struct CSNode{
    ElemType data;
    struct CSNode *firstchild, *nextsibling;
}CSNode, *CSTree;

遍历方法​

没有中序遍历是因为节点的度不一致，树的度不一定最大为2

  • 先序遍历：
    • 访问根；
    • 从左到右，访问每棵子树
  • 后序遍历：
    • 从左到右，访问每棵子树；
    • 访问根。

二叉树​

定义​

度⩽2\leqslant 2的有序树

存储表示​

//---二叉树的顺序存储表示---//
#define MAXTSIZE 100
typedef TElemType SqBiTree[MAXTSIZE];
SqBiTree bt;

//---二叉树的二叉链表存储表示---//
typedef struct BiTNode{
    TElemType data;
    struct BiTNode *lchild, *rchild;
}BiTNode, *BiTree;

名词​

  • 完美二叉树：除了叶子，每个节点度都为2，叶子都在同一层
    • 国内叫“满二叉树”
  • 完满二叉树：除了叶子，每个节点度都为2
  • 完全二叉树：叶子层可以不满的完美二叉树，并且叶子向左靠拢

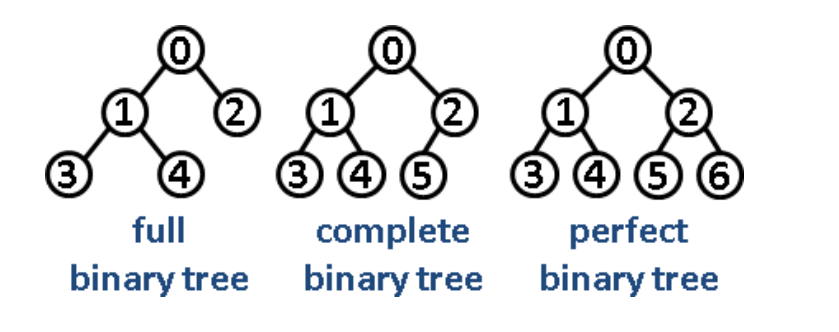
三棵树的图片

  • 二叉排序树、二叉搜索树、二叉查找树：左子树任意节点值<根节点值<右子树任意节点值

二叉树的遍历​

  • 前序遍历
    1. 访问根
    2. 访问左子树
    3. 访问右子树
  • 中序遍历
    1. 访问左子树
    2. 访问根
    3. 访问右子树
  • 后序遍历
    1. 访问左子树
    2. 访问右子树
    3. 访问根

查找树的中序遍历是有序数列

给定中序+前/后序则可以确定二叉树结构
前提：元素不重复
但是前序+后序不行，因为无法区分左右子树
中序提供左右子树区分，前后序提供根节点

规则：待补充……

线索二叉树​

定义​

遍历的前驱和后继的信息就叫线索
线索二叉树就是把线索存入每个节点里的二叉树
这样在遍历的时候空间复杂度就是O(1)O(1)了（因为可以不使用栈，遍历返回根节点需要递归）

教科书里为了省空间，就只在度小于2的节点存储
并且只在没有子树的一边存储线索

LTag==0 ? lchild=左孩子 : lchild=前驱
RTag==0 ? rchild=右孩子 : rchild=后继

存储表示​
//---线索二叉树存储表示---//
typedef struct BiThrNode{
    TElemType data;
    struct BiThrNode *lchild, *rchild;
    int LTag, RTag;
}BiThrNode, *BiThrTree;

度为2的节点在线索二叉树中：

线索二叉树前序中序后序
找前驱FTT
找后继TTF

注意：
节点输出自身时对应遍历中“访问根”的步骤
只有中序线索二叉树是完善的
因为遍历不需要前驱，所以前序可以不用栈遍历
后序线索二叉树仍需栈来遍历（纯纯的124）

哈夫曼树​

哈夫曼树（赫夫曼树、最优树）详解

定义​

当用n个结点（都做叶子结点且都有各自的权值）试图构建一棵树时
如果构建的这棵树的带权路径长度最小
称这棵树为“哈夫曼树”（“最优二叉树”，“赫夫曼树”）。

哈夫曼树示例

这颗树的带权路径长度为： WPL=7×1+5×2+2×3+4×3WPL = 7\times1 + 5\times2 + 2\times3 +4\times3

存储表示​
//---哈夫曼树的存储表示---//
typedef stuct{
    int weight;
    int parent, lchild, rchild;
}HTNode, *HuffmanTree;

名词​

  • 路径：一个结点到另一个结点之间的通路
  • 路径长度：在一条路径中，每经过一个结点，路径长度都要加1
  • 结点的权(Weight)：结点上的一个有意义的数值
  • 结点的带权路径长度：根结点到该结点的路径长度×\times该结点的权
  • 树的带权路径长度(WPL)：所有叶子结点的带权路径长度之和

构建​

不对左右子树做规定，所以
对于相同的一组权值，哈夫曼树不唯一

对于给定的有各自权值的 n 个结点：

  1. 选出两个权值最小的结点组成一个新的二叉树，根结点权值为两权值的和
  2. 在原有的n个权值中排除最小的两个权值，同时将新二叉树根节点的权值加入到 n–2 个权值的行列中
  3. 重复1和2，直到所有结点构建成一棵二叉树

构建示例

这里其实有个容易陷入的误区，就是
选了两个节点组成树了之后，下一次不一定选这棵树的根节点来组队
应该仍然选剩下权值里最小的两个
这样构建的哈夫曼树就不是图中看起来那样往一边倒的样子了

编解码​

(无)前缀编码​

要设计长度不等的编码
则必须使任一字符的编码都不是另一个字符的编码的前缀

编码​

什么样的前缀码能使得电文总长最短？
哈夫曼编码

  1. 将字符作为哈夫曼树的叶子结点，出现次数作为权值
  2. 构造哈夫曼树
  3. 结点的左分支标0，右分支标１。
  4. 将根到叶子的路径上的标号连接起来，就是该叶子代表的字符的编码．

构建完成后
则：

  • ∵∀x,y{x,y∈LeafNodes}, P(x,y)=x不为y的子节点\because\forall x,y\lbrace x,y\in LeafNodes\rbrace ,\space P(x,y)=x不为y的子节点
    ∴前缀不重复\therefore 前缀不重复
  • 权值越大，离根节点越近，编码就越短

对于编解码来说，前后所用的哈夫曼树需要完全一致

森林​

m(m⩾0)m(m\geqslant0)个不相交的树组成的集合

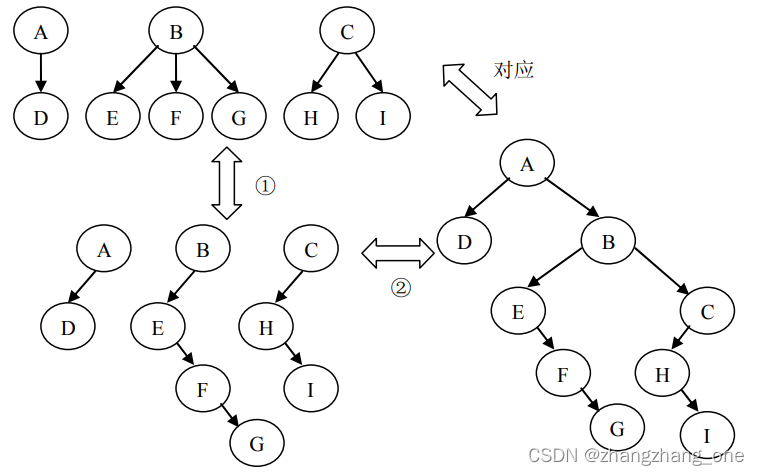
森林和二叉树的转换​

用二叉树表示法，先将所有树转换为二叉树
然后将每棵树的根节点看成兄弟
从第一棵树开始，每个根节点的右子树都是森林中的另一棵树

其实我感觉这种混沌的表示方法应该斜着看，这样兄弟节点就在一行上面了

森林转换为二叉树示例

森林的遍历（递归定义）

  • 前序遍历
    1. 访问根
    2. 访问子树
    3. 访问剩余的树构成的森林
  • 中序遍历
    1. 访问子树
    2. 访问根
    3. 访问剩余的树构成的森林
  • 后序遍历
    1. 访问子树
    2. 访问剩余的树构成的森林
    3. 访问根