图
Graph
定义
图是由顶点集合(Vertex)及顶点间的关系集合E组成的一种数据结构
记为
通用名词
-
顶点:图的最小单元权:边上的一个有意义的数值网:带权的图边:两顶点间的关系,无向图中记作弧:有向图的边,记作,x为弧尾,y为弧头
-
子图:设和,若且,则称为的子图邻接点:有边,则互为邻接点,也称相邻接;边依附于,也称边与相关联度:和该顶点相关的边的数量入度:以该顶点为弧头的弧的数量出度:以该顶点为弧尾的弧的数量
路径:一个顶点到另一个顶点之间的通路(箭头方向要相同)路径长度:一条路径中边的数量简单路径:顶点不重复出现的路径
回路(环):第一个顶点和最后一个顶点相同的路径简单回路(简单环):除了第一个顶点和最后一个顶点,路径中的其余点不重复出现的路径
-
有向图,无向图:有向图单向箭头,无向图双向箭头完全图:任意两顶点间都有边的图连通图:任意两顶点间都有路径的图连通:两顶点间有路径,称该两顶点连通连通分量:不是连通图的无向图中符合连通图的性质的子图强连通图:任意两顶点间都有来回路径的有向图强连通分量:不是强连通图的有向图中符合强连通图的性质的子图
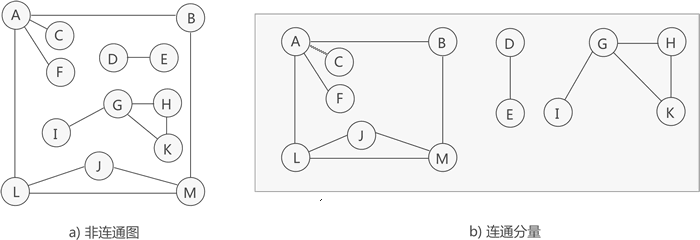
-
有向树:满足下列条件的有向图- 有且仅有一个结点入度为0
- 除根外的结点入度为1
- 从根到任一节点只有一条有向通路
生成树:对连通图进行遍历,过程中所经过的边和顶点的组合构成的树生成森林:非连通图的生成树的集合
稀疏图,稠密图:一个比较模糊的概念,稀疏图大概是的图,就是边远少于点的图,反之就是稠密图
最小生成树
最小生成树可能不唯一
定义
在遍历连通网时,总权值最小的生成树
求最小生成树
原理
- 一棵生成树与对应的图有如下性质:
- 图的所有顶点都在生成树中
- 生成树的边的数量为n-1
所以由此可得
- 要构造一棵最小生成树
- 将图中的边按权值升序排列
- 按次序选出不成环且覆盖所有顶点的边的集合
- 选到n-1条边的时候结束(因为大于n-1的时候一定成环)
这里是无后效性的,贪就完事了
Prim是从顶点开始,而Kruskal是从边开始
所以才有稠密稀疏适用性不同的说法
Prim算法
稠密图适用

步骤
- 为空集,选择任一顶点移到中
- 找出边满足
- 权值最小
- 将该边连接的顶点加入A中
- 跳到1,直至A为全部顶点的集合,恰好可以找到N-1条边
- 找出边满足
- 这样遍历出来的树就是一棵最小生成树
Kruskal算法
稀疏图适用
步骤
- 为空集
- 找出边满足
- 权值最小
- 将该边连接的顶点加入A中
- 跳到1,直至A为全部顶点的集合,恰好可以找到N-1条边
- 找出边满足
- 这样遍历出来的树就是一棵最小生成树
存储结构
存储稠密图时,使用邻接矩阵
存储稀疏图时,使用邻接表
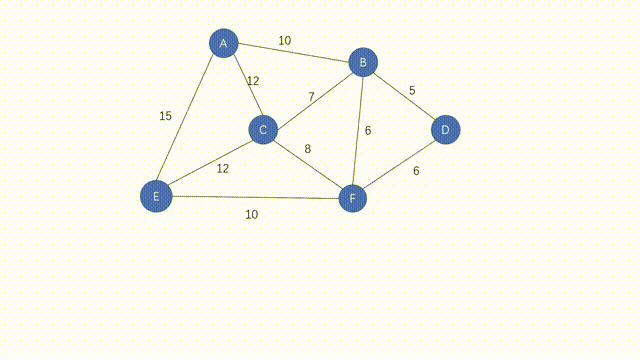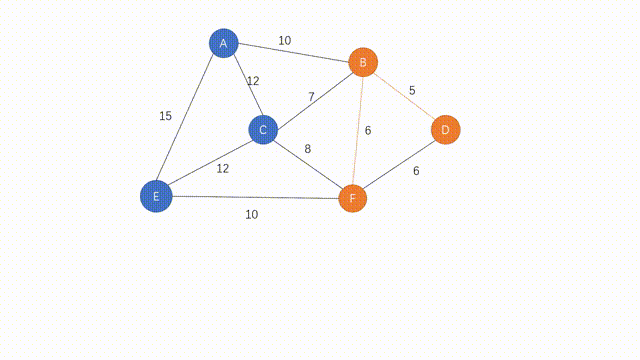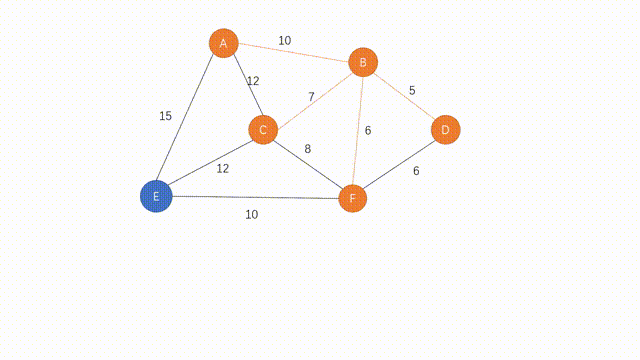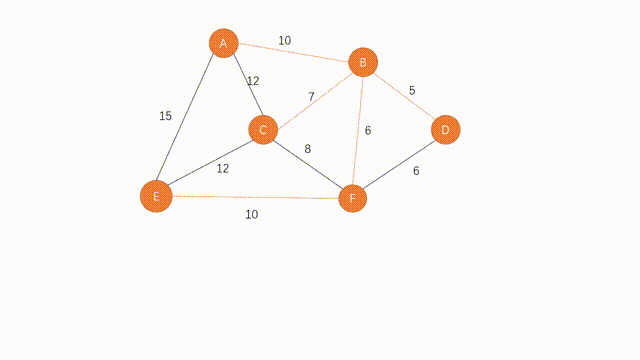
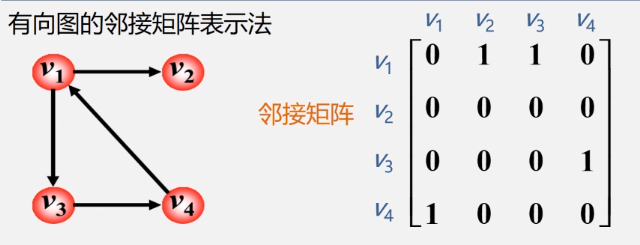
邻接矩阵
定义
设是具有个顶点的图,则的邻接矩阵是具有如下性质的阶方阵:
说人话就是
建立一个的矩阵
如果和有边(弧)的话
就在的位置上标1,反之标0
如果是网
那么就标权值,反之�标
(为编程中允许的,比任何权值都大的数)
- 无向图

- 无向图的邻接矩阵是个对称矩阵
- 有向图
存储表示
//---图的邻接矩阵存储表示---//
#define MaxInt 32767//极大值
#define MVNum 100//最大顶点数
typedef char VerTexType;//数据类型
typedef int ArcType;//权值类型
typedef struct{
VerTexType vexs [MVNum] ;//顶点表
ArcType arcs[MVNum][MVNum] ;//邻接矩阵
int vexnum, arcnum;//图的点数和边数
}AMGraph;
优缺点
- 优点
- 便于判断两顶点是否有边
- 便于计算顶点的度
- 缺点
- 不便于增删顶点
- 不便于统计边的数目
- 空间复杂度高
邻接表
定义
邻接表反映的是顶点的出度邻接情况
逆邻接表反映了顶点的入度邻接情况
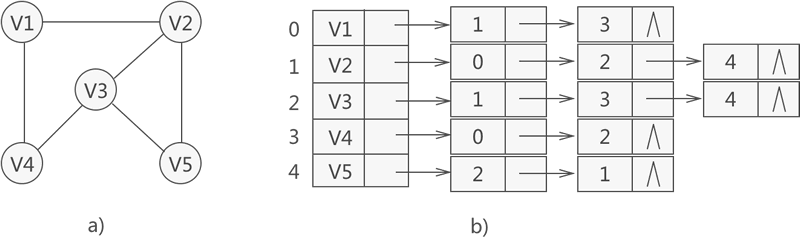
以下是邻接表的示例
- 将所有顶点存储到线性表中
- 为每个顶点配备一个单链表
- 在该单链表中存储该顶点关联边(弧)的信息
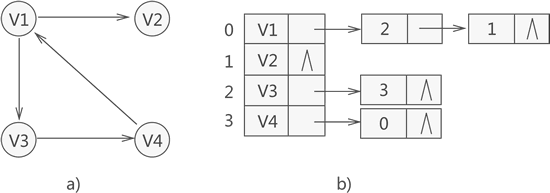
如图
以顶点为例,它的单链表中有两个结点
存储的值分别是2和1
2,1分别是,顶点在线性表中的下标
两节点分别表示两条弧。
节点构成

- 顶点节点
data:存一些没啥用的信息first:指向链表第一个元素
- 弧节点
adjvex:弧头下标nextarc:链表的下一个元素info:一些信息(可能是权值)
存储表示
//---图的邻接表存储表示---//
#define MVNum 100//最大顶点数
typedef struct ArcNode{//边
int adjvex;//该边所指向的顶点
struct ArcNode *nextarc;//指向下一条边
OtherInfo info;//信息(比如权重)
}ArcNode;
typedef struct VNode{//顶点
VerTexType data;//顶点信息
ArcNode *firstarc;//指向第一条边
}VNode, AdjList[MVNum];//AdjList表示邻接表类型
typedef struct{
AdjList vertices;
int vexnum, arcnum;//图的顶点数和边数
}ALGraph;
优缺点
- 优点
- 便于增删顶点
- 便于统计边的数目
- 空间复杂度低
- 缺点
- 不便于判断两顶点是否有边
- 不便于计算顶点的度
十字链表
最好用来存储有向图
定义
邻接表和逆邻接表的结合
- 将所有顶点存储到线性表中
- 为每个顶点配备两个单链表
- 一个链表记录以当前顶点为弧头的弧
另一个链表记录以当前顶点为弧尾的弧 - 每条边有两个指向下一条关联边的指针(见下,节点构成)
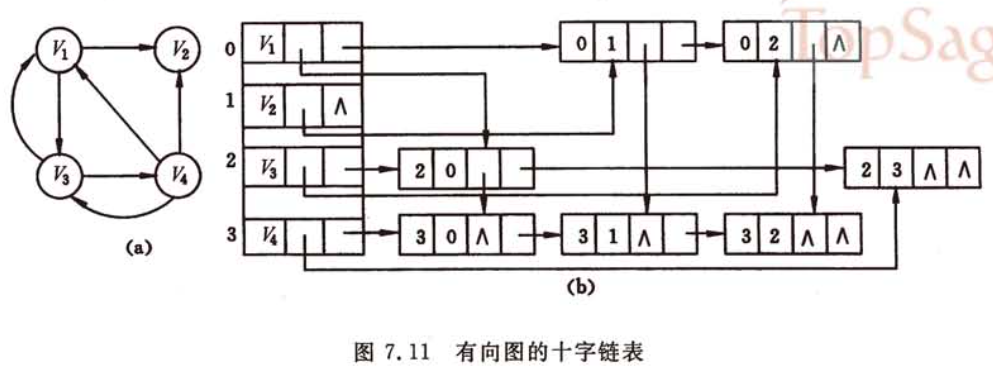
可能会有个疑问,在这张图片中
十字链表各个节点到底是怎么指的这么乱的?
其实,该图中的节点是以
弧尾下标为行
弧头下标为列
进行排列的
所以,节点的指向先从线性表开始
该行的弧全是以该顶点为弧尾的弧
然后,再从线性表依次看
将firstin指向该顶点作为弧头对应的列的第一个弧节点
最后,竖着看,从上到下把弧节点连起来
该列的弧全是以该弧头为弧头的弧
这张图中的整个表就构建完了
其实在真实情况下它不一定给你按照从小到大,从左到右的顺序输入
这个时候就是先输入的先被连接
当一个弧节点被输入进来时
先将其接到对应弧尾的顶点节点的tlink链表的最末端
后将其接到对应弧头的顶点节点的hlink链表的最末端
节点就添加完成了
代码和逻辑不复杂
就是��加弧的时候分别在两个顶点的尾链表和头链表push
但是画成图就很复杂
看起来就是错综复杂到处飞线的样子
结合了邻接矩阵和邻接表的优点
节点构成

- 顶点节点
data:存一些没啥用的信息firstin:第一条以当前顶点为弧头的弧firstout:第一条以当前顶点为弧尾的弧
- 弧节点
tailvex:弧尾下标headvex:弧头下标hlink:弧头相同的下一条弧tlink:弧尾相同的下一条弧info:一些信息(可能是权值)
这里写成"thht"而非"thth"是因为在画图理线的时候比较顺
存储表示
//---图的十字链表存储表示---//
#define MAX_VERTEX_NUM 20 //图中顶点的最大数量
//弧结点
typedef struct ArcBox {
int tailvex, headvex; //弧尾、弧头下标
struct ArcBox* hlink, * tlink;
InfoType info; //存储弧相关信息的指针
}ArcBox;
//顶点节点
typedef struct VexNode {
VertexType data; //顶点的数据域
ArcBox* firstin, * firstout;
}VexNode;
//十字链表
typedef struct {
VexNode xlist[MAX_VERTEX_NUM]; //存储顶点的顺序表
int vexnum, arcnum; //顶点数和弧数
}OLGraph;
邻接多重表
专门存储无向图的存储结构
因为在邻接表中存储无向图的时候
一条边被存储了两次
这样会存在很多的重复空间和操作
于是邻接多重表就诞生了
定义
- 将所有顶点存储到线性表中
- 为每个顶点配备一个单链表
- 在该单链表中存储该顶点关联边的信息
- 每条边有两个指向下一条关联边的指针(见下,节点构成)
- 邻接表存储无向图
- 邻接多重表存储无向图
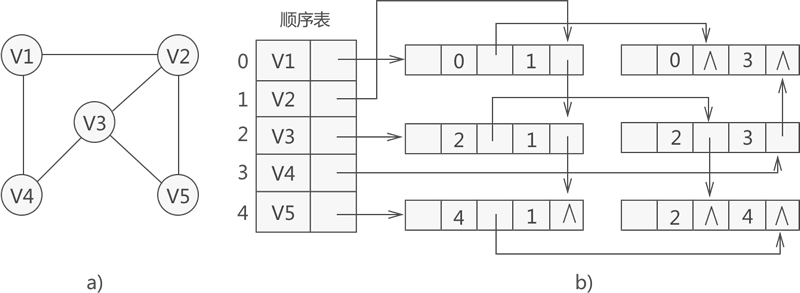
和十字链表的理解是差不多的
也是加边的时候分别在两个相关顶点的链表push
节点构成
- 顶点节点
data:存一些没啥用的信息firstedge:第一条与该顶点关联的边
- 弧节点
mark:待补充……(这个书上说的是访问标记,避免重复遍历用的)ivex,jvex:与该边有关的两顶点ilink:下一个与ivex有关的边jlink:下一个与jvex有关的边info:存储一些信息,比如权值
存储表示
#define MAX_VERTEX_NUM 20 //图中顶点的最大数量
typedef enum { unvisited, visited }VisitIf; //边标志域
//表示链表中的各个结点
typedef struct EBox {
VisitIf mark; //标志域
int ivex, jvex; //边两边顶点在顺序表中的位置下标
struct EBox* ilink, * jlink; //分别指向与ivex、jvex相关的下一个边结点
InfoType* info; //边的其它信息
}EBox;
//存储图��中的各个顶点
typedef struct VexBox {
VertexType data; //顶点数据域
EBox* firstedge; //指向当前顶点对应的链表
}VexBox;
//表示邻接多重表结构
typedef struct {
VexBox adjmulist[MAX_VERTEX_NUM]; //存储图中顶点的顺序表
int vexnum, edgenum; //记录图中的顶点数量和边数量
}AMLGraph;
最短路径算法
两顶点路径中总权值最小的一条路径称为最短路径